Калькулятор 4

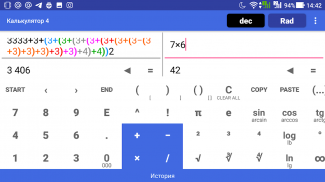
Egyszerű és funkcionális számológép

Kiemeli a zárójeleket színnel

Egy kattintással bezárhatja a zárójelbe tett kifejezést, vagy megváltoztathatja a jelet

Számol útközben

Sorban több függvény írható zárójelek nélkül, például lglg10000000000 = 1

ÚJ az 1.8.3-as verzióban:

➤ A befogási funkciók bevitele

➤Csökkentette a billentyűzet gombjainak számát és megváltoztatta azok helyét

➤A billentyűzet néhány szavát vektoros ikonok helyettesítik

ÚJ az 1.8.2-es verzióban:

➤A minimális támogatott Android verzió 5,0 Lollipop-ra nőtt

➤Nincsenek speciális változtatások, főleg a kód refaktorozása, hogy később megkönnyítsük a módosításokat :)

EwÚj felület a gombok átméretezéséhez

➤ Hozzáadott indító képernyő

➤ A beállítások előbeállításai a párbeszédpanelekben

➤Új tervezési beállítások

➤A történelem átkerült az adatbázisba

➤ Néhány témát fejlesztettek

➤Az eredménymező teljes kattintással elérhető

ÚJ az 1.8.1 változatban:

OreTovábbi témák

ManagerA menedzser visszavonása befejeződött

➤ A zárójelbe csomagolás funkció befejeződött

➤ Hozzáadta a jel megváltoztatásának funkcióját (később befejezem)

ÚJ az 1.8.0 verzióban:

➤Témák

➤ Testreszabható eredményformátum (számelválasztók és E)

➤UNDO / REDO - egy művelet visszavonása / megismétlése - 100 változásra emlékszik

➤sgn - signum - egy szám előjelét adja vissza (-1 vagy 0 vagy 1)

➤A API javítása 16-ra, mostantól támogatja az android 4.1.1+ verziót

A működéshez, illetve az eltávolításhoz és az újratelepítéshez SZÜKSÉGES TÖRÖLNI ezeket az alkalmazásokat

➤Vízszintes görgetési válasz

➤A billentyűzet szövegmérete a gombok magasságához igazodik

➤arc most visszatér a fokkal, ha kapcsoló = deg

➤Csomagolás zárójelbe gomb (nyomja meg többször a zárójelek magasabb szintre helyezéséhez. Nyomja meg a kurzor előtti kifejezés zárójelezéséhez)

➤ Hozzáadta a szöveg törlésének lehetőségét egy gomb lenyomásával

ExpressionVáltozott kifejezésfeldolgozási logika:

például most:

• √9 (9) = √ (9) × (9) = 27, de √9e = √ (9 × e)

• sinπcosπ = (sin (π)) × (cos (π)), de sin2πcosπ = (sin (2 × π)) × (cos (π))

• cos2π = cos (2 × π)

• 2 ^ 2e = 2 ^ (2e), de 2 ^ 2lg100 = 2 ^ 2 × lg100

• √lg10000 (1E5) = √ (log (10000)) × (1E5)

• lg4! 4 = lg (4!) × 4

• lg4! Lg100 = lg (4!) × lg100

Általánosságban elmondható, hogy ha a függvény argumentum a számok implicit szorzata (előjel nélküli szorzás), akkor az összes szám szerepel a függvény argumentumban

•••••••••

• 2³! = (2 ^ 3)!

• lg100³ = lg100 ^ 3 = (lg100) ^ 3

• lg100³! = (lg100³)!

➤ még sok apró vizuális változás és fejlesztés